La nouvelle IA de Musk a résolu un problème millénaire mais a été arrêtée d’urgence ? Pourquoi cette « blague » a-t-elle tenu la communauté IA éveillée toute la nuit ?

Grok-3 a-t-il prouvé « l’hypothèse de Riemann » ?
Un tweet publié par le chercheur de xAI Hieu Pham ce week-end a provoqué un tollé dans le cercle de l'IA. Les mots originaux du tweet étaient les suivants :
Le système d'IA Grok-3 vient de prouver l'hypothèse de Riemann. Pour vérifier l'exactitude de cette preuve, nous avons décidé de suspendre la formation du système. Si la preuve se confirme, nous ne poursuivrons plus sa formation, car une telle IA est considérée comme trop intelligente et peut constituer une menace pour l'homme.
Comme c’est l’ancienne règle, parlons d’abord de la conclusion. Ce n’est qu’une blague.
Cependant, à mesure que les tweets continuaient de fermenter, ils ont rapidement suscité l'attention et les discussions de plus de deux millions d'internautes, et ont même rayonné vers les cercles d'opinion publique d'IA au pays et à l'étranger.
L'origine de l'affaire remonte probablement à une "révélation" antérieure de l'internaute Andrew Curran, qui affirmait qu'un incident catastrophique s'était produit lors de l'entraînement de Grok-3.
Par la suite, toutes sortes de rumeurs bizarres se sont succédées.
Les internautes ont hué le fait que le PDG d'OpenAI, Sam Altman, ait pointé un énorme laser sur le plus grand cluster de formation de xAI, provoquant une grave corruption des données ; certains ont également sérieusement suggéré que quelqu'un sabotait délibérément l'opération de formation LLM de nouvelle génération.
Il y a même des blagues selon lesquelles l'IA semble avoir pris conscience d'elle-même et résolu l'hypothèse de Riemann, mais "15 points-virgules ont été délibérément omis" dans le code de preuve, ce qui rend impossible la vérification par les humains.

Même le fondateur de Runway, Cristóbal Valenzuela, est venu se joindre à la fête :
Gen-4 vient de remporter tous les Oscars, y compris celui du meilleur film. Afin d'approfondir ses réalisations innovantes dans le domaine de l'art, nous avons décidé de suspendre sa formation. Si le film est effectivement aussi révolutionnaire que le prétendent les premières critiques, nous ne reprendrons pas la formation car il montre que l’IA a atteint un niveau de compétence artistique si élevé qu’elle pourrait menacer la créativité humaine.
Les rumeurs ne cessaient de s’aggraver.
De nombreux chercheurs de xAI ont également relayé les tweets d'Andrew Curran pour rejoindre ce « grand team building » collectif.
Par exemple, notre vieille connaissance, co-créateur de xAI, Greg Yang, a d'abord plaisanté en disant que Grok-3 avait soudainement battu le vieux garde de sécurité du bureau pendant l'entraînement.
Un autre chercheur, Heinrich Kuttler, a déclaré : « Oui, la situation était très mauvaise ! Nous avons ensuite remplacé tous les poids anormaux par nan (Not a Number, non-number) avant de récupérer. »
Bien sûr, des internautes plus rationnels ont directement interrogé la version actuelle de Grok sur X sur sa compréhension de l'hypothèse de Riemann. Comme prévu, la performance de Grok était très « Makabaka ».
En fin de compte, la farce a été mise fin par l'instigateur, le chercheur de xAI Hieu Pham :
Bon, Saturday Night Live est terminé. Quant à savoir pourquoi prouver l’hypothèse de Riemann est dangereux, je recommande vivement l’excellent roman Humans de Matt Haig (@matthaig1).
La question est donc la suivante : pourquoi la nouvelle selon laquelle Grok-3 prouve l’hypothèse de Riemann attire-t-elle une large attention ? La première est l’importance de l’hypothèse de Riemann elle-même.
L'hypothèse de Riemann est une conjecture importante sur la distribution des nombres premiers en mathématiques. Elle a été proposée par le mathématicien allemand Bernhard Riemann en 1859. La conjecture est répertoriée comme un projet de recherche du Clay Mathematics Institute.

Il s'agit de la fonction zêta de Riemann, qui est définie comme :
ζ(s)=1+12s+13s+14s+⋯zeta(s) = 1 + frac{1}{2^s} + frac{1}{3^s} + frac{1}{4 ^s} + cdotsζ(s)=1+2s1+3s1+4s1+⋯
Le contenu principal de l'hypothèse de Riemann est le suivant : la partie réelle des points zéro de toutes les fonctions zêta de Riemann non triviales est égale à 1/2. En d'autres termes, si ss est un point zéro non trivial de la fonction zêta de Riemann, c'est-à-dire ζ(s)=0ζ(s)=0, alors sa partie réelle doit être ℜ(s)=1/2ℜ(s )=1/2 .
Le Clay Mathematics Institute a déclaré que si quelqu'un parvenait à prouver l'hypothèse de Riemann, il décernerait un prix d'un million de dollars. Cependant, cette conjecture n’a pas été prouvée ou réfutée jusqu’à présent, et elle est largement considérée comme un mystère non résolu dans la théorie moderne des nombres.

La preuve de cette conjecture a eu des conséquences considérables pour la théorie des nombres, une branche des mathématiques.
Actuellement, de nombreuses technologies de chiffrement modernes (telles que la protection des paiements en ligne, la confidentialité des données, etc.) reposent sur les propriétés des nombres premiers. Prouver l’hypothèse de Riemann pourrait permettre aux humains de mieux comprendre les fondements de ces technologies et pourrait affecter les futurs algorithmes de sécurité.
Si Grok-3 peut prouver l’hypothèse de Riemann, cela favorisera non seulement des progrès substantiels dans les domaines des mathématiques théoriques, de la physique, de la cryptographie et d’autres domaines, mais marquera également un énorme progrès dans le raisonnement de l’IA et la résolution de problèmes complexes.
On peut même dire que cela deviendra un événement marquant pour que l’intelligence artificielle dépasse l’intelligence humaine.

Yang Zhilin, fondateur de Dark Side of the Moon, a déclaré un jour que les scénarios mathématiques sont les scénarios les plus idéaux pour entraîner la capacité de réflexion de l’IA.
Les mathématiques sont un système logique extrêmement rigoureux, et les capacités de raisonnement de l’IA reposent souvent sur des déductions logiques rigoureuses.
Le processus par lequel l’IA résout des problèmes mathématiques est essentiellement un processus de réflexion continu. Dans ce processus, elle continuera à essayer différentes idées et à trouver la bonne réponse par des essais et des erreurs répétés. Même si des erreurs surviennent lors des calculs, l’IA peut corriger les résultats grâce à la vérification et à la relecture.

Un concept similaire se reflète également dans la formation d’apprentissage par renforcement d’OpenAI o1.
Si les grands modèles précédents étaient des données d’apprentissage, o1 ressemble davantage à un apprentissage de la pensée. Tout comme lorsque nous résolvons un problème, nous devons non seulement écrire la réponse, mais aussi le raisonnement. Vous pouvez mémoriser une question par cœur, mais si vous apprenez à raisonner, vous pouvez tirer des conclusions.
Par conséquent, lors du test AIME de cette année destiné aux lycéens exceptionnels aux États-Unis, GPT-4o n'a répondu qu'à 13 % des questions. En comparaison, la précision de o1 atteint 83 points de pourcentage.
En termes d'évaluation de la recherche scientifique GPQA Diamond au niveau doctorat, GPT-4o a obtenu un score de 56,1 %, tandis que o1 a obtenu des résultats encore meilleurs. Non seulement il a battu 69,7 % des docteurs humains, mais il a également atteint un taux de précision de 78 %.
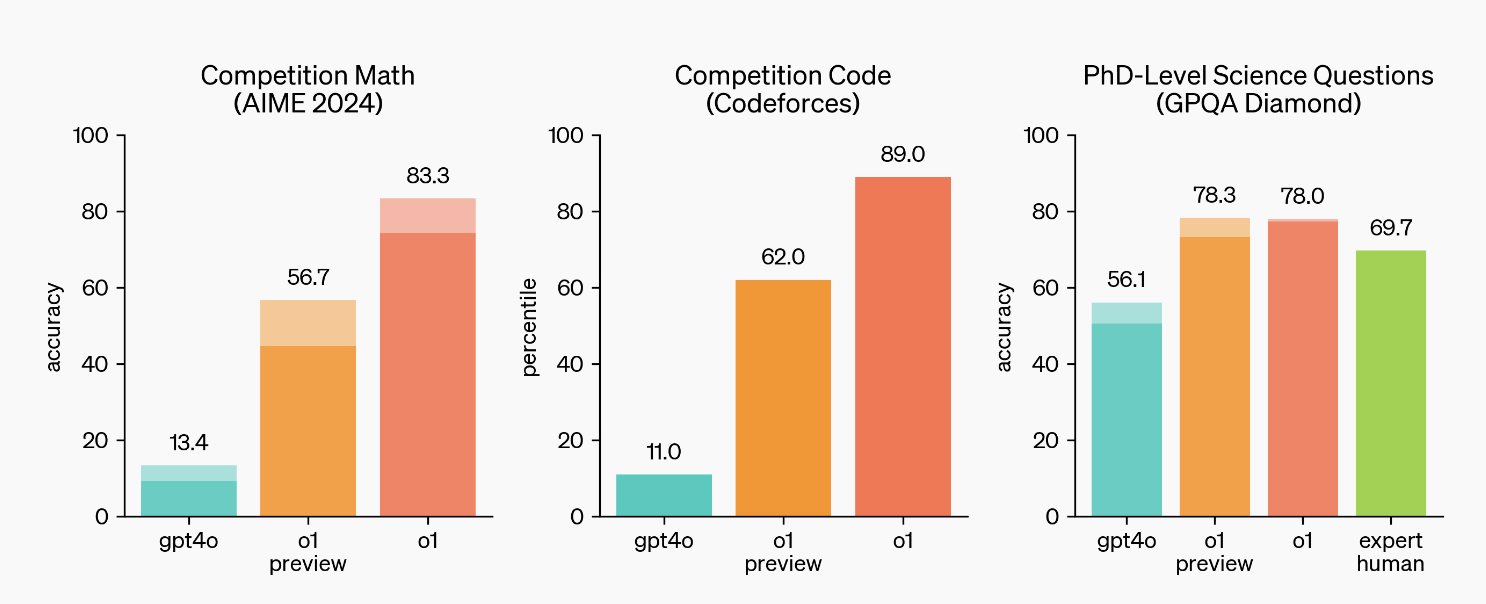
Lors de l'évaluation de l'Olympiade internationale d'informatique (IOI), lorsque 50 tentatives étaient autorisées pour chaque question, le modèle a obtenu un taux de score de 49 %, soit 213 points, et lorsque les possibilités de soumission pour chaque question ont été augmentées à 10 000 fois, sa finale Le score s'est amélioré à 362 points.
C’est plus facile à comprendre avec l’analogie d’AlphaGo, qui a battu le champion du monde de Go.
AlphaGo est formé par apprentissage par renforcement. Il utilise d'abord un grand nombre de records d'échecs humains pour un apprentissage supervisé, puis joue aux échecs contre lui-même, dans chaque partie, il est récompensé ou puni en fonction de la victoire ou de la défaite, améliorant ainsi continuellement ses compétences aux échecs. et même maîtriser des méthodes auxquelles les joueurs d'échecs humains ne peuvent pas penser.

o1 et AlphaGo sont similaires, mais AlphaGo ne peut jouer qu'à Go, tandis que o1 est un grand modèle de langage à usage général.
Le matériel que o1 apprend peut être des banques de questions mathématiques, des codes de haute qualité, etc. Ensuite, o1 est formé pour générer une chaîne de pensée pour résoudre des problèmes, et sous le mécanisme de récompense ou de punition, il génère et optimise sa propre chaîne de pensée pour améliorer continuellement son capacité de raisonnement.
Cela explique en fait pourquoi OpenAI met l'accent sur les fortes capacités mathématiques et de codage de o1, car il est plus facile de vérifier le bien et le mal, et le mécanisme d'apprentissage par renforcement peut fournir un retour d'information clair, améliorant ainsi les performances du modèle.
Bien entendu, le plus important est de savoir comment étendre cette capacité de raisonnement à un plus large éventail de domaines.
Par conséquent, nous verrons de nombreux internautes étrangers applaudir Grok-3 pour prouver l'hypothèse de Riemann : « Si tel est le cas, nous assistons vraiment à une énorme avancée. »
Musk a exagéré à plusieurs reprises la puissance de Grok-3 en public. Il a affirmé que Grok-3 devrait être commercialisé avant la fin de l'année et qu'il deviendra "l'IA la plus puissante au monde".
En fait, Grok-3 est la troisième génération de modèles de langage à grande échelle développés par la startup d'IA xAI mentionnée ci-dessus, et devrait surpasser tous les grands modèles d'IA existants en termes de performances.
La raison en est que la formation Grok-3 s'appuie sur Colossus, le plus grand cluster de formation en IA au monde.

Le cluster se compose de 100 000 GPU NVIDIA H100 refroidis par liquide, utilisant une seule architecture d'interconnexion réseau RDMA. La taille de ce cluster a dépassé celle de tout autre supercalculateur dans le monde et le nombre de GPU continuera d'augmenter à l'avenir.
Selon un rapport de The Information, l'émergence de Colossus a même attiré l'attention d'Altman, qui a envoyé un avion survoler la base d'entraînement de Colossus pour tenter d'espionner les progrès de son développement et son approvisionnement en énergie.

Par conséquent, lorsque les trois éléments de « l'IA la plus puissante », du « problème mathématique millénaire » et de l'éternelle « théorie de la menace de l'IA » se superposent, une parfaite « tempête de rumeurs » se forme.
On peut même penser que la rumeur selon laquelle Grok-3 aurait prouvé l’hypothèse de Riemann n’est pas tant une farce qu’un miroir pour l’ensemble de l’industrie de l’IA :
La première est que cela reflète l'attitude profondément ancrée des gens à l'égard de l'IA. Un grand nombre d'optimistes technologiques croient fermement que l'IA finira par devenir omnipotente. Ils craignent qu'elle se développe de manière incontrôlable si elle se développe trop rapidement. il ne se développera pas assez vite pour réaliser des percées.
La seconde est que depuis l’avènement du GPT-4, même si de nouveaux produits ont continué à émerger dans le domaine de l’IA, il y a eu peu de véritables avancées.
Les êtres humains ne sont pas seulement les créateurs de l’IA, mais aussi son public le plus anxieux.

Derrière chaque rumeur sur l’IA se cache l’anxiété et les attentes de l’ensemble du secteur.
Associée au récent tollé concernant le développement de Scaling Law qui heurte un mur, par rapport à la période explosive de l'année dernière, la « fatigue de l'innovation » de cette année a fait perdre patience aux petites améliorations du modèle.
En ce sens, la rumeur selon laquelle Grok-3 aurait prouvé l’hypothèse de Riemann est également devenue une imagination collective des gens pour l’avenir. Même en tant qu'utilisateurs ordinaires, nous attendons de plus en plus avec impatience le prochain moment de changement qualitatif de GPT-3.5 à GPT-4.
Bien entendu, les véritables avancées en matière d’IA se produisent souvent lorsque personne n’est optimiste à leur sujet.
Mais nous espérons tous que le mystère sera révélé avant la fin de l’année.
# Bienvenue pour suivre le compte public officiel WeChat d'Aifaner : Aifaner (ID WeChat : ifanr). Un contenu plus passionnant vous sera fourni dès que possible.
Ai Faner | Lien original · Voir les commentaires · Sina Weibo
