Heaps vs. Stacks : qu’est-ce qui les distingue ?
En tant que programmeur, vous avez probablement rencontré les termes « tas » et « pile ». C'est une pratique répandue pour les débutants d'utiliser ces deux termes de manière interchangeable et incorrecte.
Bien que les étudiants d'un cours sur les structures de données et les programmeurs expérimentés fassent facilement la distinction entre ces deux structures de données, elles peuvent sembler identiques pour les autres.
Les programmeurs doivent différencier les deux et les utiliser de manière appropriée dans des situations de programmation pratiques. Les intervieweurs sont souvent désireux de donner aux candidats un scénario, puis de demander la structure de données la plus appropriée.
Continuez à lire pendant que nous examinons en détail les tas, les piles, leurs différences et les applications pertinentes.
Qu'est-ce qu'un tas ?
Un tas pour les programmeurs est généralement une structure de données arborescente spéciale souvent appelée « file d'attente prioritaire ». Les tas qui sont une structure arborescente binaire complètement équilibrée (rappelez-vous que tous les niveaux d'un arbre binaire complet sont remplis sauf le dernier niveau) et qui suivent une propriété de tas sont appelés tas binaires.
La propriété heap structure l'arborescence de manière à placer la valeur maximale ou minimale à la racine.
Dans un Max Heap, la valeur des nœuds parents est supérieure à celle des nœuds enfants et la racine de l'arborescence contient la valeur maximale. Alternativement, un Min Heap est structuré pour avoir la valeur minimale en tant que racine, et chaque nœud enfant a une valeur supérieure à celle de son parent. La propriété de tas doit être vraie de manière récursive pour chaque nœud de l'arbre binaire.
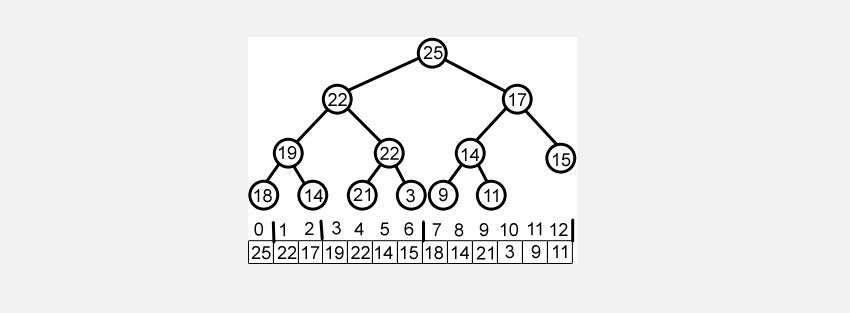
Les tas sont généralement implémentés via des tableaux linéaires, le premier élément du tableau ( Arr[0] ) représentant la racine. Pour un nœud spécifique i , vous pouvez récupérer les nœuds enfants à Arr[ (2*i) + 1 ] et Arr[ (2*i) + 2] , de même le nœud parent est situé à Arr[ (i-1) /2 ] index. La plupart des langages tels que Java et C++ contiennent des bibliothèques qui fournissent aux utilisateurs des tas min et max prêts à l'emploi.
Qu'est-ce qu'une pile ?
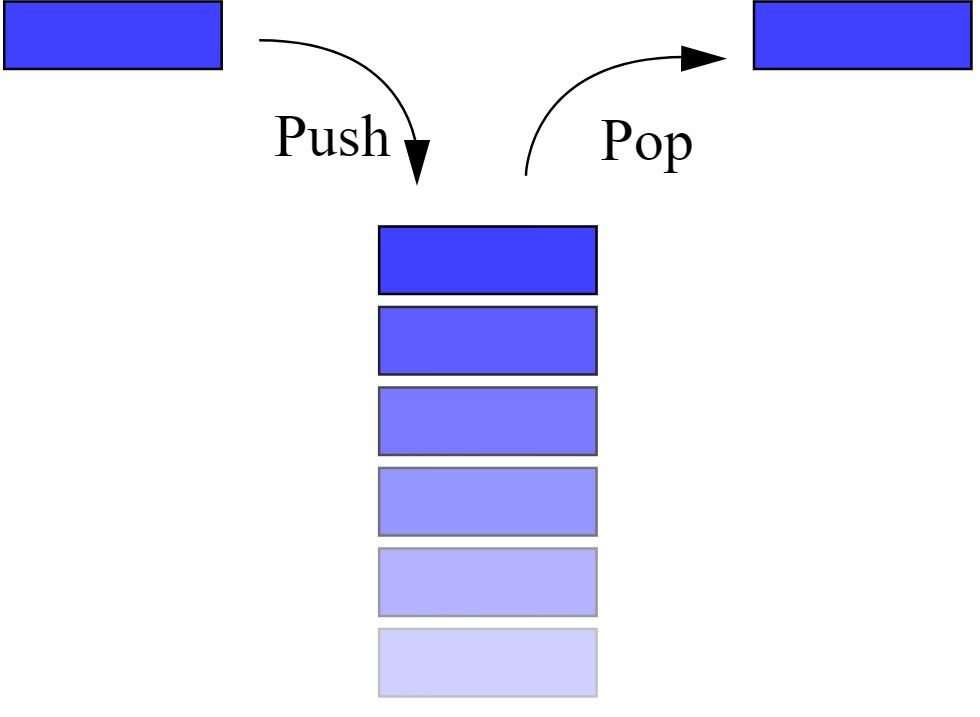
Les piles sont l'une des premières structures de données enseignées aux étudiants, et elles ne doivent pas être négligées. Une pile est une structure de données qui se comporte comme n'importe quelle pile réelle (cartes, plaques, etc.). Les piles n'autorisent les opérations qu'à une extrémité et, par conséquent, elles ont une caractéristique LIFO (Last-In-First-Out). En revanche, les files d'attente ont une caractéristique FIFO (First-In-First-Out) et permettent des opérations aux deux extrémités.
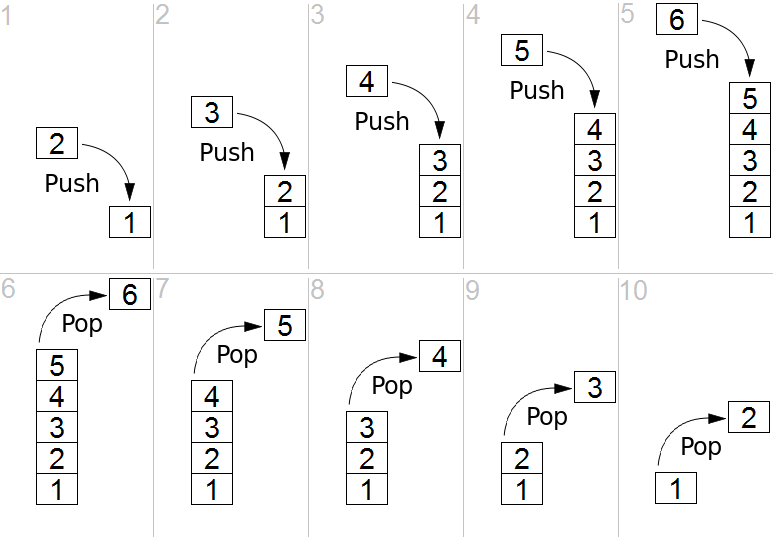
Les opérations de pile typiques consistent en push (insertion de données dans le haut de la pile) et pop (suppression de l'élément de données le plus haut). Vous pouvez implémenter des piles via des pointeurs, des tableaux ou même des listes chaînées, selon vos besoins. C++, C# et Java contiennent tous des bibliothèques qui ont déjà implémenté une pile, vous pouvez donc les utiliser quand vous en avez besoin.
Tas contre piles
Si vous avez lu jusqu'ici, vous avez une assez bonne idée des différences entre une pile et un tas. Les piles sont linéaires et ont une caractéristique LIFO, tandis que les tas ont une structure arborescente et suivent la propriété de tas. Ils ont tous deux des applications différentes dont nous parlerons dans la section suivante.
En termes d'analyse de complexité temporelle asymptotique, vous pouvez construire un tas binaire en O(n) et extraire la valeur minimale ou maximale en O(1). Les insertions et les suppressions peuvent être réalisées en temps O(log N). En revanche, l'insertion et la suppression prennent 0 (1) temps dans une pile.
Applications typiques
Pour les raisons évoquées ci-dessus, les tas sont très efficaces lorsqu'ils sont utilisés comme file d'attente prioritaire. Les algorithmes de graphes tels que Minimum Spanning Tree de Prim et Dijkstra's Shortest Path utilisent généralement des tas comme file d'attente prioritaire. Une autre application importante des tas est de trier efficacement un tableau en un temps O(N logN); cette technique de tri est connue sous le nom de "Heap Sort".
Les piles ont également une variété d'applications critiques telles que la gestion de la mémoire et l'évaluation des expressions. Si vous rencontrez un problème de codage de retour en arrière, il peut être judicieux de sauver la journée en utilisant une pile.
Prioriser les structures de données
Tout programmeur à succès vous dira l'importance de maîtriser les structures de données. C'est une excellente idée d'essayer de comprendre et de se familiariser avec l'utilisation de différentes structures de données au fur et à mesure des besoins, car c'est un concept vital pour tout programmeur.
