Une introduction à l’algorithme de tri par fusion
Le tri par fusion est un algorithme de tri basé sur la technique du « diviser pour régner ». C'est l'un des algorithmes de tri les plus efficaces.
Dans cet article, vous découvrirez le fonctionnement de l'algorithme de tri par fusion, l'algorithme du tri par fusion, sa complexité temporelle et spatiale et son implémentation dans divers langages de programmation tels que C++, Python et JavaScript.
Comment fonctionne l'algorithme de tri par fusion ?
Le tri par fusion fonctionne sur le principe du diviser pour régner. Le tri par fusion divise à plusieurs reprises un tableau en deux sous-tableaux égaux jusqu'à ce que chaque sous-tableau se compose d'un seul élément. Enfin, tous ces sous-tableaux sont fusionnés de telle sorte que le tableau résultant soit trié.
Ce concept peut être expliqué plus efficacement à l'aide d'un exemple. Considérons un tableau non trié avec les éléments suivants : {16, 12, 15, 13, 19, 17, 11, 18}.
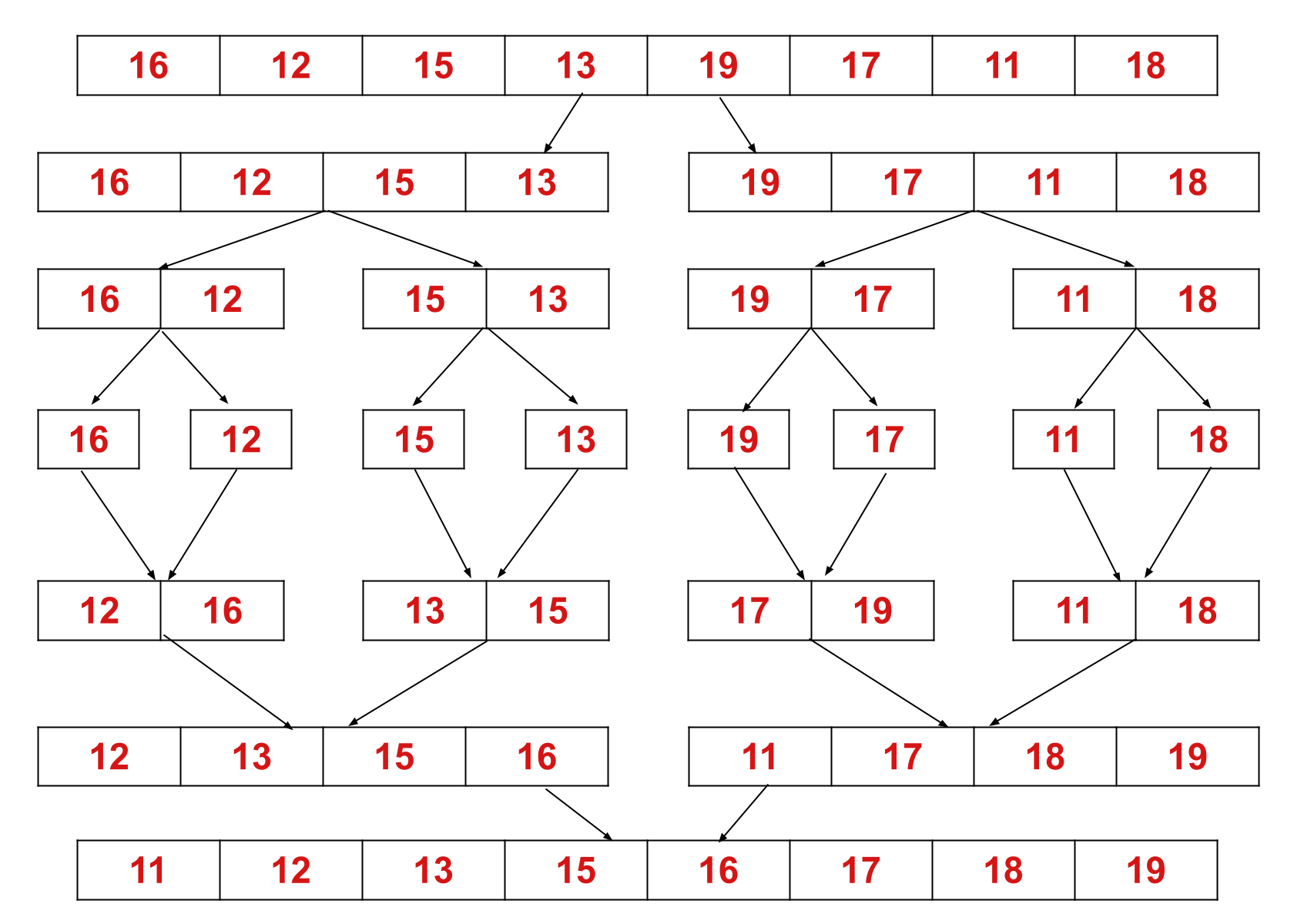
Ici, l'algorithme de tri par fusion divise le tableau en deux moitiés, s'appelle lui-même pour les deux moitiés, puis fusionne les deux moitiés triées.
Algorithme de tri de fusion
Ci-dessous l'algorithme du tri par fusion :
MergeSort(arr[], leftIndex, rightIndex)
if leftIndex >= rightIndex
return
else
Find the middle index that divides the array into two halves:
middleIndex = leftIndex + (rightIndex-leftIndex)/2
Call mergeSort() for the first half:
Call mergeSort(arr, leftIndex, middleIndex)
Call mergeSort() for the second half:
Call mergeSort(arr, middleIndex+1, rightIndex)
Merge the two halves sorted in step 2 and 3:
Call merge(arr, leftIndex, middleIndex, rightIndex)
Complexité temporelle et spatiale de l'algorithme de tri par fusion
L'algorithme de tri par fusion peut être exprimé sous la forme de la relation de récurrence suivante :
T(n) = 2T(n/2) + O(n)
Après avoir résolu cette relation de récurrence à l'aide du théorème du maître ou de la méthode de l'arbre de récurrence, vous obtiendrez la solution sous la forme O(n logn). Ainsi, la complexité temporelle de l'algorithme de tri par fusion est O(n logn) .
La complexité temporelle dans le meilleur des cas du tri par fusion : O(n logn)
La complexité en temps moyen du cas du tri par fusion : O(n logn)
La complexité temporelle dans le pire des cas du tri par fusion : O(n logn)
La complexité de l' espace auxiliaire de l'algorithme de tri par fusion est O(n) car n espace auxiliaire est requis dans la mise en œuvre du tri par fusion.
Implémentation en C++ de l'algorithme de tri par fusion
Vous trouverez ci-dessous l'implémentation C++ de l'algorithme de tri par fusion :
// C++ implementation of the
// merge sort algorithm
#include <iostream>
using namespace std;
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
void merge(int arr[], int leftIndex, int middleIndex, int rightIndex)
{
int leftSubarraySize = middleIndex - leftIndex + 1;
int rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
int L[leftSubarraySize], R[rightSubarraySize];
// Copying data to temporary arrays L[] and R[]
for (int i = 0; i < leftSubarraySize; i++)
L[i] = arr[leftIndex + i];
for (int j = 0; j < rightSubarraySize; j++)
R[j] = arr[middleIndex + 1 + j];
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
int i = 0;
// Initial index of Right subarray
int j = 0;
// Initial index of merged subarray
int k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int leftIndex, int rightIndex)
{
if(leftIndex >= rightIndex)
{
return;
}
int middleIndex = leftIndex + (rightIndex - leftIndex)/2;
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 16, 12, 15, 13, 19, 17, 11, 18 };
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Unsorted array:" << endl;
printArray(arr, size);
mergeSort(arr, 0, size - 1);
cout << "Sorted array:" << endl;
printArray(arr, size);
return 0;
}Production:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19Implémentation JavaScript de l'algorithme de tri par fusion
Vous trouverez ci-dessous l'implémentation JavaScript de l'algorithme de tri par fusion :
// JavaScript implementation of the
// merge sort algorithm
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
function merge(arr, leftIndex, middleIndex, rightIndex) {
let leftSubarraySize = middleIndex - leftIndex + 1;
let rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
var L = new Array(leftSubarraySize);
var R = new Array(rightSubarraySize);
// Copying data to temporary arrays L[] and R[]
for(let i = 0; i<leftSubarraySize; i++) {
L[i] = arr[leftIndex + i];
}
for (let j = 0; j<rightSubarraySize; j++) {
R[j] = arr[middleIndex + 1 + j];
}
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
var i = 0;
// Initial index of Right subarray
var j = 0;
// Initial index of merged subarray
var k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
function mergeSort(arr, leftIndex, rightIndex) {
if(leftIndex >= rightIndex) {
return
}
var middleIndex = leftIndex + parseInt((rightIndex - leftIndex)/2);
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
function printArray(arr, size) {
for(let i = 0; i<size; i++) {
document.write(arr[i] + " ");
}
document.write("<br>");
}
// Driver code:
var arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ];
var size = arr.length;
document.write("Unsorted array:<br>");
printArray(arr, size);
mergeSort(arr, 0, size - 1);
document.write("Sorted array:<br>");
printArray(arr, size);Production:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19
Implémentation Python de l'algorithme de tri par fusion
Vous trouverez ci-dessous l'implémentation Python de l'algorithme de tri par fusion :
# Python implementation of the
# merge sort algorithm
def mergeSort(arr):
if len(arr) > 1:
# Finding the middle index of the array
middleIndex = len(arr)//2
# Left half of the array
L = arr[:middleIndex]
# Right half of the array
R = arr[middleIndex:]
# Sorting the first half of the array
mergeSort(L)
# Sorting the second half of the array
mergeSort(R)
# Initial index of Left subarray
i = 0
# Initial index of Right subarray
j = 0
# Initial index of merged subarray
k = 0
# Copy data to temp arrays L[] and R[]
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i = i + 1
else:
arr[k] = R[j]
j = j + 1
k = k + 1
# Checking if there're some remaining elements
while i < len(L):
arr[k] = L[i]
i = i + 1
k = k + 1
while j < len(R):
arr[k] = R[j]
j = j + 1
k = k + 1
# Function to print the elements
# of the array
def printArray(arr, size):
for i in range(size):
print(arr[i], end=" ")
print()
# Driver code
arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ]
size = len(arr)
print("Unsorted array:")
printArray(arr, size)
mergeSort(arr)
print("Sorted array:")
printArray(arr, size)
Production:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19Comprendre d'autres algorithmes de tri
Le tri est l'un des algorithmes les plus utilisés en programmation. Vous pouvez trier des éléments dans différents langages de programmation à l'aide de divers algorithmes de tri tels que le tri rapide, le tri à bulles, le tri par fusion, le tri par insertion, etc.
Le tri à bulles est le meilleur choix si vous souhaitez en savoir plus sur l'algorithme de tri le plus simple.
