Comment utiliser le tri par sélection
Le tri par sélection est une technique de tri qui sélectionne un élément de la liste, puis échange sa place avec un autre. Il sélectionne le plus gros élément, puis l'échange avec un élément de l'index le plus élevé de la liste.
L'algorithme le fait à plusieurs reprises jusqu'à ce que la liste soit triée. Si vous n'êtes pas sûr du fonctionnement du tri par sélection, vous êtes au bon endroit. Nous l'expliquerons plus en détail ci-dessous, en vous montrant un exemple.
Tri de la sélection : un examen plus approfondi
Supposons que vous ayez la liste : [39, 82, 2, 51, 30, 42, 7]. Pour trier la liste à l'aide du tri par sélection, vous devez d'abord trouver le nombre le plus élevé.
Avec la liste donnée, ce nombre est 82. Échangez 82 avec le nombre dans l'index le plus élevé (c'est-à-dire 7).
Après le premier passage, le nouvel ordre de liste sera : [39, 7, 2, 51, 30, 42, 82]. Chaque fois que l'algorithme parcourt toute la liste, cela s'appelle un "pass".
Notez que la liste maintient une sous-liste triée et une sous-liste non triée pendant le processus de tri.
La liste d'origine commence par une liste triée de zéro éléments et une liste non triée de tous les éléments. Puis après le premier passage, il a une liste triée n'ayant que le numéro 82.
Au deuxième passage, le numéro le plus élevé de la sous-liste non triée sera 51. Ce numéro sera échangé contre 42 pour donner le nouvel ordre de liste ci-dessous :
[39, 7, 2, 42, 30, 51, 82].
Le processus est répété jusqu'à ce que toute la liste soit triée. La figure ci-dessous résume l'ensemble du processus :
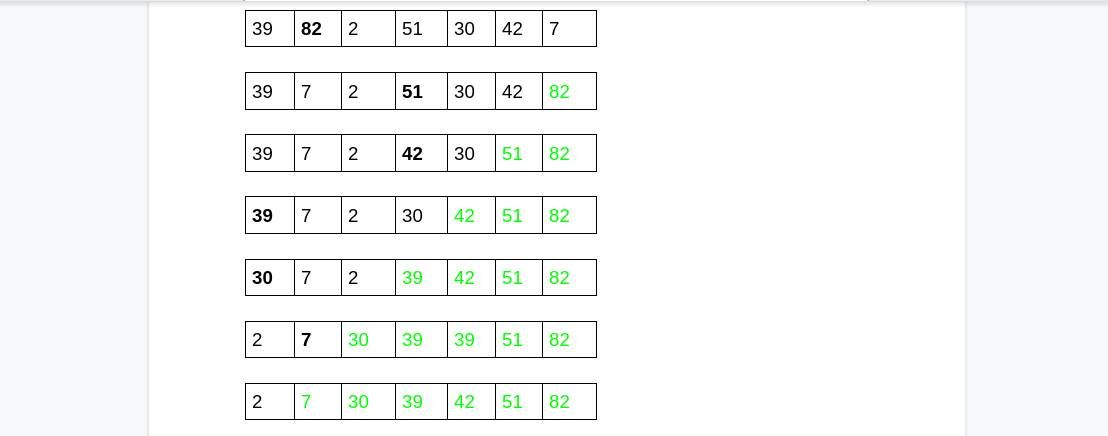
Les nombres en gras noir indiquent la valeur de liste la plus élevée à ce moment-là. Ceux en vert montrent la sous-liste triée.
Analyse d'algorithmes
Pour obtenir la complexité (en utilisant la notation Big-O) de cet algorithme, suivez ci-dessous :
Au premier passage, (n-1) comparaisons sont effectuées. Au deuxième passage, (n-2). Au troisième passage, (n-3) et ainsi de suite jusqu'au (n-1)ième passage qui ne fait qu'une comparaison.
En résumant les comparaisons ci-dessous, on obtient :
(n-1)+ (n-1)+ (n-1)+…+1 = ((n-1)n)/2.
Par conséquent, le tri par sélection est O(n 2 ).
Implémentation du code
Le code montre les fonctions que vous pouvez utiliser pour effectuer un tri par sélection à l'aide de Python et Java.
Python:
def selectionSort(mylist):
for x in range(len(mylist) - 1, 0, -1):
max_idx = 0
for posn in range(1, x + 1):
if mylist[posn] > mylist[max_idx]:
max_idx = posn
temp = mylist[x]
mylist[x] = mylist[max_idx]
mylist[max_idx] = tempJava:
void selectionSort(int my_array[]){
for (int x = 0; x < my_array.length - 1; x++)
{
int index = x;
for (int y = x + 1; y < my_array.length; y++){
if (my_array[y] < my_array[index]){
index = y; // find lowest index
}
}
int temp = my_array[index]; // temp is a temporary storage
my_array[index] = my_array[x];
my_array[x] = temp;
}}Passer du tri par sélection au tri par fusion
Comme l'analyse de l'algorithme ci-dessus l'a montré, l'algorithme de tri par sélection est O(n 2 ). Il a une complexité exponentielle et est donc inefficace pour des ensembles de données très volumineux.
Un bien meilleur algorithme à utiliser serait le tri par fusion avec une complexité de O(nlogn). Et maintenant que vous savez comment fonctionne le tri par sélection, la prochaine étape de votre liste d'étude pour les algorithmes de tri devrait être le tri par fusion.
